Kafelkowania, Drzewa, Wyznaczniki

 

• Na ile sposóbów można pokryć prostokąt \(m \times n\) kostkami domina (tak, jak na rysunku po prawej)? Liczba ta wynosi:  

(1)                                                                                                       \(\prod_{j=1}^{m} \prod_{k=1}^{n} (4cos^2\frac{\pi j}{m+1} + 4cos^2\frac{\pi k}{n+1})^{1/4}\)

"To jakiś kosmos! Dlaczego to w ogóle jest liczba całkowita?! Skąd iloczyn cosinusów?" - po warsztatach będziemy wiedzieć dlaczego ;)

• Ile drzew rozpinających ma zadany graf? Odpowiedzi udziela twierdzenie Kirchhoffa o drzewach rozpinających (Matrix Tree Theorem) - wystarczy policzyć wyznacznik macierzy zwanej laplasjanem grafu.

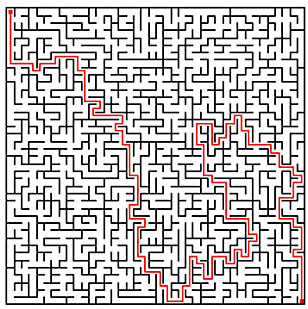
Zobaczymy też, jaki związek mają drzewa rozpinające z sieciami elektrycznymi i błądzeniami losowymi i dlaczego przydaje się to do generowania labiryntów takich, jak ten:

 

 

 

 

 

 

 

Zależnie od ilości czasu przewidziane są też desery.

 

Program zajęć

Poniższy plan to program maksimum. Poza dwoma głównymi problemami wspomnianymi powyżej zdążymy zapewne omówić tylko niektóre z dodatkowych tematów (oznaczonych [*]).

• wyznacznik macierzy, podstawowe własności, wartości własne macierzy
• zliczanie skojarzeń w grafach, permanent macierzy
• macierz Kasteleyna, zliczanie kafelkowań na kratce \(m \times n\)
• [*] metoda zliczania skojarzeń na ogólnym grafie planarnym
• [*] bijekcja Temperleya
• laplasjan grafu, twierdzenie Kirchhoffa o drzewach rozpinających
• sieci elektryczne i błądzenia losowe, losowe drzewa rozpinające a opór zastępczy, łańcuchy Markowa
• [*] generowanie losowych drzew rozpinających: algorytmy Aldousa-Brodera i Wilsona, labirynty
• [*] więcej zabaw wyznacznikiem: lemat Gessela-Viennota i jego zatosowania
• [*] więcej o kafelkowaniach: Aztec Diamond, asymptotyczny kształt losowego kafelkowania, "Arctic Circle Theorem"
• [*] algorytmy szukanie skojarzeń oparte na wyznaczniku

Wymagania

Rozumieć podstawową terminologią związaną z grafami i wiedzieć coś o liczbach zespolonych (wystarczy wiedzieć, co to pierwiastek \(n\)-tego stopnia z jedynki). Nie trzeba wiedzieć nic o algebrze liniowej, aczkolwiek oczywiście jeśli ktoś widział wcześniej macierze i wyznaczniki, to będzie miał łatwiej.

Zadania kwalifikacyjne

Należy spróbować rozwiązać jak najwięcej zadań - oczekuję, że każdy rozwiąże co najmniej pięć zadań spośród zadań 1-6 oraz co najmniej dwa z zadań 7-10 (aczkolwiek próg kwalifikacji będzie zależał od poziomu nadesłanych rozwiązań). Jeśli zadania okażą się trudne, daj znać, a zamieszczę wskazówki. Podobnie, jeśli zadania okażą się zbyt banalne, daj znać, a zamieszczę trudniejsze wersje.

Rozwiązania należy wysyłać na adres: michal.kotowski1@gmail.com. Zachęcam do ich wcześniejszego przysyłania (nie tuż przed deadlinem) - będzie możliwość poprawiania rozwiązań. Jeśli masz jakiekolwiek pytania, wątpliwości, zauważysz błąd w treści zadania etc. - koniecznie napisz!

Zadanie 1

a) Wyobraźmy sobie prostokąt \(2 \times n\), który chcemy pokryć kostkami domina o wymiarach \(2 \times 1\) (każda kostka może być ustawiona pionowo lub poziomo). Na ile sposobów można to zrobić?

b) Spróbuj zastosować podobną metodę, co w podpunkcie a), do analogicznego problemu dla prostokąta \(3 \times n\).

Zadanie 2

Rozważmy prostokąt i kafelkowanie kostkami domina z poprzedniego zadania. O kostce domina możemy myśleć jako o krawędzi łączącej dwa sąsiednie punkty kratki\(2 \times n\). Jeśli weźmiemy dwa kafelkowania i nałożymy je na siebie, to dostaniemy pokrycie prostokąta cyklami o parzystej długości (dwie nałożone na siebie krawędzie dają wtedy cykl długości dwa), tak jak na (nieco niechlujnym) rysunku:

 

a) Podać przykład, że dwie różne pary kafelkowań mogą dawać to samo pokrycie cyklami.

b) Wymyślić, w jaki sposób można zorientować krawędzie prostokąta, aby zorientowane pokrycie cyklami wyznaczało już jednoznacznie parę zorientowanych kafelkowań. Wykorzystać wynik z podpunktu a) poprzedniego zadania do wyznaczenia liczby wszystkich takich zorientowanych pokryć cyklami. [Wskazówka: wystarczy zorientować pionowe krawędzie]

Zadanie 3

Rozważmy zbiór \(\{ 1,2,...,n\}\) i wszystkie jego permutacje. Transpozycją nazwiemy permutację, która zamienia miejscami dwa ustalone elementy, a pozostałych nie rusza.

a) Pokazać, że każdą permutację można zapisać jako złożenie pewnej liczby transpozycji.

b) Znakiem permutacji \(\sigma\) nazwiemy liczbę równą \(+1\), jeśli \(\sigma\) daje się rozłożyć na parzystą liczbę transpozycji, oraz \(-1\), jeśli daje się rozłożyć na nieparzystę liczbę transpozycji. Pokazać, że liczba ta jest dobrze określona, tj. dana permutacja nie może mieć jednocześnie znaku \(+1\) i \(-1\).

Zadanie 4

Rozważmy nieskierowany graf \(G\) o parzystej liczbie wierzchołków. Doskonałym skojarzeniem nazwiemy taki zbiór krawędzi, że ich końce pokrywają wszystkie wierzchołki grafu i każdy wierzchołek należy do tylko jednej krawędzi. Cykl parzystej długości \(C\) nazwiemy dobrym, jeśli po wyrzuceniu wierzchołków należących do tego cyklu pozostała część grafu posiada przynajmniej jedno doskonałe skojarzenie.

Rozważmy teraz dowolną orientacją krawędzi grafu \(G\). Powiemy, że cykl parzystej długości \(C\) jest nieparzyście zorientowany, jeśli obchodząc go w dowolnym kierunku przechodzimy przez nieparzyście wiele krawędzi zgodnych z wybraną orientacją grafu\(G\).

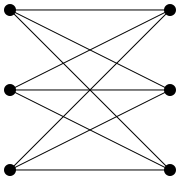
Podać przykład grafu posiadającego co najmniej dwa cykle, który można zorientować tak, aby zachodziła następująca własność: każdy dobry cykl jest nieparzyście zorientowany. Pokazać, że grafu \(K_{3,3}\), przedstawionego poniżej, nie da się zorientować w ten sposób.

 

Zadanie 5

Pokazać, że:

\(\prod_{l=1}^{n} cos(\frac{l \pi}{2n+1})= 2^{-n}\)                                      (2)

Zadanie 6

Rozważmy układ dwóch równań o rzeczywistych lub zespolonych współczynnikach \(a,b,c,d\) :

\( ax+by = 0 \\ cx + dy = 0 \\ \)                                                       (3)

 

Oczywiście \(x = y = 0\) zawsze jest jego rozwiązaniem. Znaleźć warunek konieczny i dostateczny na współczynniki, aby istniały inne, niezerowe rozwiązania. Czy potrafisz uogólnić ten warunek na przypadek trzech równań? A na \(n\) równań?

Zadanie 7

Drzewem rozpinającym w grafie nazwiemy podzbiór jego krawędzi, który jest drzewem (czyli grafem spójnym bez cykli) oraz zawiera wszystkie wierzchołki grafu. Znaleźć liczbę wszystkich drzew rozpinających w drabince o wysokości \(n\) (poniżej znajduje się przykładowy rysunek dla \(n=8\):

(uwaga - graf traktujemy jako etykietowany, tj. liczy się nie tylko "kształt" drzewa, ale też to, jakie wierzchołki zawiera)

Zadanie 8

Graf \(G\) nazwiemy planarnym, jeśli da się go narysować na płaszczyźnie tak, aby krawędzie się nie przecinały. Ścianą takiego grafu nazwiemy dowolny spójny obszar ograniczony krawędziami, w szczególności uwzględniamy zewnętrzną, nieskończoną ścianę (od tej pory utożsamiamy graf z jego rysunkiem na płaszczyźnie). Grafem dualnym do\(G\) nazwiemy graf \(G^{*}\) otrzymany następująco: dla każdej ściany \(f\) w \(G\) wprowadzamy jeden wierzchołek \(f^{*}\) w \(G^{*}\) i dla każdej krawędzi, którą stykają się ściany \(f_{1}\) i \(f_{2}\) w \(G\), odpowiadające im wierzchołki \(f_{1}^{*}\),\(f_{2}^{*}\) w \(G^{*}\) łączymy krawędzią.

Pokazać, że dla grafu planarnego zachodzi wzór Eulera:

(4)           \(V - E + F = 2\)

 
gdzie \(V\) to liczba wierzchołków, \(E\), a \(F\) - liczba ścian.

Wskazówka: dualność oraz drzewa rozpinające.

(można tego wzoru dowodzić też przez indukcję, ale zachęcam do próby użycia wskazówki)

Zadanie 9

Rozważmy dla \(n \geq 3\) następujący układ równań:

\(x_{1} + x_{3} = \lambda x_{2} \\ x_{2} + x_{4} = \lambda x_{3} \\ ...\\ x_{n-2} + x_{n} = \lambda x_{n-1} \\ x_{n-1} + x_{1} = \lambda x_{n} \\ x_{n} + x_{2} = \lambda x_{1} \\ \)                                        (5)

 

gdzie \(\lambda\) jest pewnym parametrem. Znaleźć wszystkie rozwiązania w zależności od \(\lambda\). Wskazówka: układ równań ma cykliczną symetrię - jak mogą tu pomóc zespolone pierwiastki z jedynki?

Zadanie 10

Znaleźć liczbę wszystkich drzew na zbiorze wierzchołków \(\{1,2,...,n\}\) (drzewa uznajemy za etykietowane, czyli liczy się nie tylko "kształt" drzewa, ale numery wierzchołków). Uwaga: to zadanie jest być może trudniejsze od pozostałych, więc w razie trudności pojawią się wskazówki.

Kontakt

Mój mail to michal.kotowski1@gmail.com - bardzo chętnie odpowiem na wszelkie pytania związane z warsztatami i nie tylko!