Kombinatoryka Podziałów
Prowadzący
Michał Kotowski
Opis
Podział liczby naturalnej \(N\) to przedstawienie jej jako sumy dodatnich składników (bez uwzględniania kolejności). Na przykład \(5 = 4+1 = 3+2 = 3+1+1\) i tak dalej. Definicja jest bardzo prosta, ale prowadzi do nietrywialnej i ciekawej matematyki. Podziały, a zwłaszcza ich reprezentacje przez diagramy Ferrersa (p. obrazek),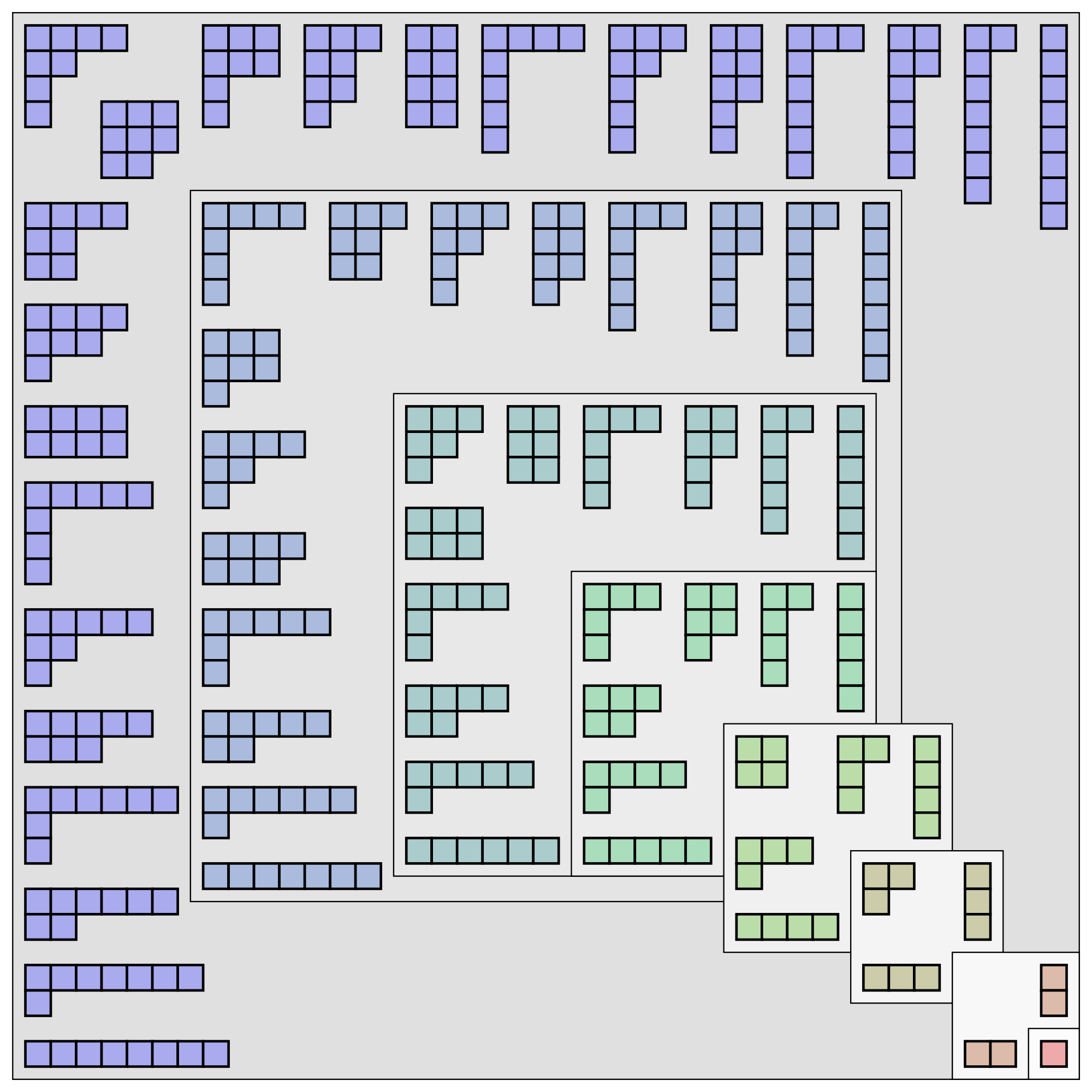 są wdzięcznym tematem do czysto kombinatorycznych dowodów bijektywnych - dowodzimy, że np. podziałów N na części nieparzyste jest tyle samo, co na części parami różne, przez podanie bijekcji między tymi dwoma klasami. Z drugiej strony, można je badać także za pomocą funkcji tworzących, czyli pewnego rodzaju szeregów formalnych zliczających obiekty kombinatoryczne. Jest to silniejsze, bardziej algebraiczne narzędzie, stanowiące także pomost między kombinatoryką a teorią liczb. Podziałami zajmował się m.in. Ramanujan, słynny matematyk o dużych osiągnięciach w teorii liczb.
są wdzięcznym tematem do czysto kombinatorycznych dowodów bijektywnych - dowodzimy, że np. podziałów N na części nieparzyste jest tyle samo, co na części parami różne, przez podanie bijekcji między tymi dwoma klasami. Z drugiej strony, można je badać także za pomocą funkcji tworzących, czyli pewnego rodzaju szeregów formalnych zliczających obiekty kombinatoryczne. Jest to silniejsze, bardziej algebraiczne narzędzie, stanowiące także pomost między kombinatoryką a teorią liczb. Podziałami zajmował się m.in. Ramanujan, słynny matematyk o dużych osiągnięciach w teorii liczb.
Program zajęć
Na zajęciach zaczniemy od zupełnie elementarnej kombinatoryki, a następnie wprowadzimy pojęcie funkcji tworzącej. Zobaczymy, że często łatwiej jest udowodnić tożsamość kombinatoryczną przez manipulacje szeregami formalnymi, ale jednocześnie dowód bijektywny daje większy wgląd w naturę problemu. Poruszymy m.in. następujące tematy:
- diagramy Ferrersa, tożsamości na różnych klasach podziałów
- twierdzenie Eulera o liczbach pięciokątnych, rekurencja na liczbę podziałów
- funkcje tworzące dla różnych klas podziałów
- tożsamość trójkowa Jacobiego i jej zastosowania
- współczynniki q-dwumianowe
- tożsamości Rogersa-Ramanujana
Jeśli starczy czasu, to możliwe, że pojawią się też bardziej zaawansowane tematy:
- tableaux Younga, związek z wielomianami symetrycznymi
- "hook length formula", zliczanie tableaux Younga
- podziały planarne
Wymagania
- podstawowe obycie w kombinatoryce (wiedzieć, co to bijekcja, dwumian Newtona)
- wiedzieć, że \(\frac{1}{1-x} = 1 + x + x^2 + ...\)
Zadania kwalifikacyjne
Zadania dzielą się na łatwiejsze i trudniejsze. Należy zrobić 5 zadań łatwiejszych i 2 trudniejsze, aczkolwiek jeśli zadania okażą się trudne, liczba ta może się zmniejszyć (p. niżej).
Rozwiązania proszę przesyłać na maila: michal.kotowski1@gmail.com (im wcześniej, tym lepiej, istnieje możliwość poprawiania rozwiązań). W razie wątpliwości co do sformułowania zadania proszę o kontakt.
Jeśli masz trudności z rozwiązaniem któregoś zadania - napisz, możliwe, że pojawią się wskazówki do zadań. Podobnie, jeśli zadania są dla Ciebie za łatwe - daj znać, a dodam trochę trudniejszych.
Zadania łatwiejsze
Zadanie 1
Podział z uwzględnianiem kolejności to przedstawienie liczby \(N \) jako sumy dodatnich składników, z uwzględnianiem ich kolejności. Np. 5=1+4=4+1 to różne podziały liczby 5. Znaleźć liczbę wszystkich takich podziałów liczby \(N\). Dla danego \(k\) znaleźć liczbę wszystkich takich podziałów \(N\), w których występuje dokładnie \(k\) składników
Zadanie 2
Znaleźć liczbę wszystkich podziałów \(N\) z uwzględnianiem kolejności, w których występuje parzyście wiele składników parzystych.
Zadanie 3
Udowodnić przez podanie interpretacji kombinatorycznej tożsamości:
a) \(\sum^n_{i=0} \left(\! \begin{array}{c} k+i \\ i \end{array} \!\right) = \left(\! \begin{array}{c} k+n+1 \\ n \end{array} \!\right) \)
b) \(\sum^n_{i=0} i \left(\! \begin{array}{c} n \\ i \end{array} \!\right) \)\(= n\cdot2^{n-1}\)
Zadanie 4
Udowodnić, że podziałów liczby \(N\) (bez uwzględniania kolejności), które mają wyłącznie parzyste składniki, jest tyle samo co takich, w których każdy składnik występuje parzyście wiele razy.
Zadanie 5
Niech \(p_k(n)\) oznacza liczbę podziałów \(n\) (bez uwzględniania kolejności) o dokładnie \(k\) składnikach. Udowodnić, że:
\(p_k(n) = p_{k-1}(n-1) + p_k(n-k)\) (1)
Zadanie 6
Wiemy, że dla dowolnego \(|x| < 1\) i \(k \geq 1\) mamy:
\(\frac{1}{1-x^k} = 1 + x^k + x^{2k} + ...\) (2)
Tego typu szeregi możemy mnożyć wyraz po wyrazie. Niech:
\(\frac{1}{1-x} \cdot \frac{1}{1-x^2}\cdot \frac{1}{1-x^5} = a_0 + a_1x + a_2x + ...\) (3)
Podać interpretację kombinatoryczną współczynnika \(a_n\) w terminach rozmieniania kwoty na monety 1-, 2- i 5-złotowe.
Zadania trudniejsze
Zadanie 7
Niech \(F_{n}\) oznacza \(n\)-tą liczbę Fibonacciego. Wyrazić w terminach liczb Fibonacciego liczbę podziałów \(N\) z uwzględnianiem kolejności takich, że:
a) każdy składnik jest większy od 1
b) każdy składnik jest równy 1 lub 2
c) każdy składnik jest nieparzysty
Zadanie 8
Rozpatrzmy wszystkie podziały liczby \(n\) z uwzględnianiem kolejności. Pokazać, że składnik \(k\) występuje we wszystkich podziałach łącznie \((n−k+3)2^{n−k−2}\) razy.
Zadanie 9
Inwersją w permutacji \(\sigma\) zbioru \(\{1,2,...,n\}\) nazywamy parę \((i,j)\) taką, że \(i<j\), ale \(\sigma (i) > \sigma(j)\). Niech \(i(\sigma)\) oznacza łączną liczbę inwersji w permutacji \(\sigma\). Pokazać, że:
\(\sum_{\sigma} x^{i(\sigma)} = (1+x)(1+x+x^2)\cdot ...\cdot(1+x+x^2 + ... + x^{n-1})\)(4)
gdzie suma jest po wszystkich permutacjach zbioru \(\{1,2,...,n\}\).
Zadanie 10
Znaleźć liczbę wszystkich podziałów (bez uwzględniania kolejności) liczby \(N\), w których każdy składnik jest równy \(1\) lub \(2\).