Struktury na Q

Damian Orlef - orlef.damian [na] gmail.com

Wstęp

Na warsztatach zajmiemy się różnorodnymi problemami o podłożu w teorii liczb, do których rozwiązania przydają się interesujące strutury porządkujące liczby wymierne.

Zadajmy sobie następujące proste pytanie: Jak wygląda zbiór liczb wymiernych? Nie zdołalibyśmy go w całości w sensowny sposób narysować na osi liczbowej, więc dla każdego kolejnego n przyjrzyjmy się ułamkom o mianownikach nie przekraczających n i zwiększajmy kolejno to ograniczenie. Otrzymamy zagęszczające się ciągi, zwane ciągami Fareya, o interesujących własnościach:

- jeśli ułamki nieskracalne \(\frac{a}{b}\) oraz \(\frac{c}{d}\) (b,d>0) w którymś z ciągów występują jako dwa kolejne wyrazy,
to \(cb - ad = 1\) (ułamki różnią się o "tak mało, jak tylko mogą") i zachodzi wynikanie przeciwne.

- każdy ciąg Fareya da się otrzymać z poprzedniego poprzez wstawienie pomiędzy niektóre pary kolejnych wyrazów ułamków według reguły "pomiędzy \(\frac{a}{b}\) i \(\frac{c}{d}\) wstaw \(\frac{a+c}{b+d}\)".

Sąsiedztwo w którymś z ciągów Fareya okazuje się więc znaczącą relacją. Od tego jak ją zaprezentujemy zależy do badania jakich problemów teorii liczb nam się ona najbardziej przyda.

- Możemy na płaszczyźnie w każdym punkcie wymiernym osi X postaci \(( \frac{p}{q} , 0)\) narysować okrąg styczny w tym punkcie do osi X - okrąg o środku w \((\frac{p}{q}, \frac{1}{2q^2})\) i promieniu \(\frac{1}{2q^2}\). Otrzymane tzw. okręgi Forda są parami styczne zewnętrznie lub rozłączne, przy czym styczność odpowiada dokładnie fareyowskiemu sąsiedztwu ułamków \(\frac{p}{q}\), które im odowiadają. Otrzymane narzędzie pozwala na poglądowe badanie twierdzeń o możliwości aproksymowania liczb niewymiernych \(\alpha\) w taki sposób, by w nierówności \([|\alpha - \frac{p}{q}| \leq \frac{C}{q^2} ]\) stała \(C\) była jak najmniejsza, a przy tej stałej \(q\) mogło być dowolnie duże. Tego typu szacowania pozwoliły łatwo wskazać pierwszy przykład liczby przestępnej.

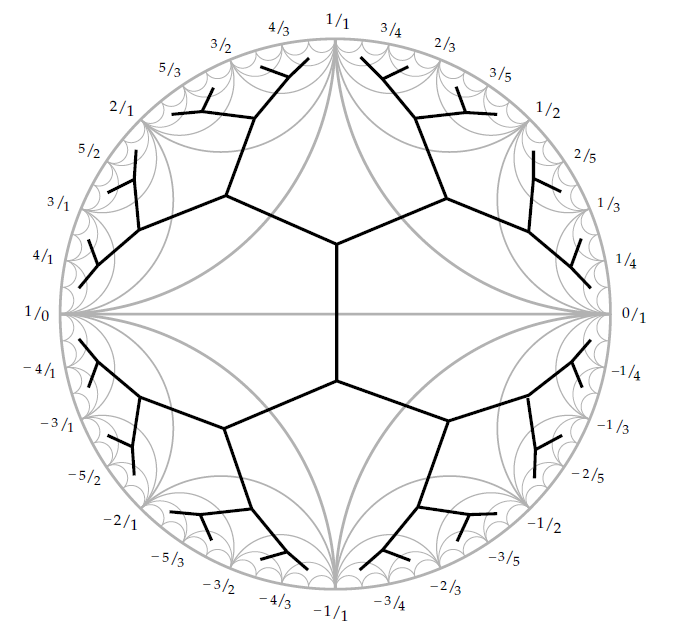
- Możemy zrzutować prostą na okrąg (uzupełniając symboliczną nieskończonością \(\frac{1}{0}\)) i relację sąsiedztwa prezentować przez odcinki (na rysunku po prawej - szare łuki). Wówczas odcinki te tworzą trójkąty, a zaznaczenie ich środków i połączenie środków trójkątów sąsiednich da nam drzewo z rysunku. Drzewa tego możemy użyć do nadania macierzom 2x2 o współczynnikach całkowitych i wyznaczniku równym 1 (macierzom utworzonym z dwóch sąsiednich ułamków) sensu jako przekształceniom tego drzewa, które przekształcają sąsiednie wierzchołki na sąsiednie (w sensie drzewa), co prowadzi do interesującej struktury samych macierzy. Po drodze zaś pozwala się zapoznać z interesującą kombinatoryką działania grup na zbiorach.

Ta ilustracja prowadzi też do graficznego badania rówania Pella \(x^2 - dy^2 =1\) przy ustalonym \(d\) oraz problemu zapisywania liczby \(n\) jako wyrażenia postaci \(x^2 + dy^2\) (ponownie z ustalonym \(d\)).

- Możemy narysować drzewo Sterna-Brocotta i mieć strukturę drzewa binarnego (informatycznie: BST) związaną blisko z rozwinięciem liczb (również niewymiernych) w ich ułamki łańcuchowe, a tym samym też z najlepszym przybliżaniem liczb rzeczywistych przy ograniczonym mianowniku.

Tematy

Zajmiemy się następującymi zagadnieniami, zależnie od czasu:

- Własności ciągów Fareya, okręgi Forda.

- Aproksymacja liczb niewymiernych, tw. Hurwitza. (Jeśli będą chętni to opowiemy też o konstruowaniu liczb przestępnych)

- Diagram Fareya i jego przekształcenia. Struktura \(SL_{2}(\mathbb{Z})\). (Być może inne podobne kombinatoryczne rozważania o działaniach grup)

- Wykorzystanie diagramu Fareya do równań diofantycznych.

- Drzewo Sterna-Brocota.

- Ciąg Calkina-Wilfa, czyli o zaskakującym ciągu zawierającym wszystkie liczby wymierne.

Wymagania i zadania kwalifikacyjne

Pojawił się skrypt przedzajęciowy.

Elementarna znajomość teorii liczb, umiejętność mnożenia macierzy 2 na 2. Pomocna będzie wiedza, co to jest grupa i co to znaczy, że grupa działa na zbiorze, ale tutaj będzie to bardziej prosta notacja niż znajomość teorii, a poza tym można o tym przeczytać w skrypcie.

Należy też rozwiązać zadania kwalifikacyjne, które są tutaj.

Bibliografia i inne do poczytania

(Na razie bibliografia, potem pojawi się niezależnie napisane opracowanie części warsztatów/skrypt)

1. Allen Hatcher, "Topology of Numbers" - książka, w której pojawia się geometria ułamków Fareya i dużo więcej

2. L. R. Ford, "Fractions" - artykuł o okręgach Forda, m.in. z dowodem tw. Hurwitza

3. J. P. Serre, "Trees" - książka o wykorzystaniu działania grup na drzewach do badania ich własności, zrobiliśmy po części z niej użytek badając działanie wprowadzone w [1]

4. Garść materiałów na "Cut the knot";

5. "Dowody z księgi" - można tutaj znaleźć artykuł o ciągu i drzewie Calkina-Wilfa

6. "Mathematical Omnibus" - można tu znaleźć dowód geometryczny zależności między kolejnymi ułamkami w ciągu Fareya przy pomocy wzoru Picka, a także trochę innych rzeczy, o których była mowa

Efekty uczenia

Uczestnik warsztatów:

- wie co to diagram Fareya.

- dostrzega ułamki w świecie wokół siebie.

- zna ograniczenia własnej wiedzy i rozumie potrzebę dalszego kształcenia, w tym zdobywania wiedzy pozadziedzinowej.

- potrafi precyzyjnie formułować pytania, służące pogłębieniu własnego zrozumienia danego tematu lub odnalezieniu brakujących elementów rozumowania.

- …