Geometryczna Teoria Grup

 Opis

Grupy pojawiają się wszędzie tam, gdzie interesują nas symetrie i ich złożenia. Przykładem grupy jest zbiór wszystkich izometrii płaszczyzny euklidesowej - izometrie można składać (a składanie jest łączne) i odwracać, w dalszym ciągu dostając izometrie -
i te własności już wystarczą, by mówić o grupie. Miejsce płaszczyzny może też zająć przestrzeń euklidesowa trój- i więcej wymiarowa. Już tutaj pojawia się kilka ciekawych pytań:

- Jak wygladają skończone zbiory izometrii, które są zamknięte na złożenia i branie odwrotności?

- Czy każde dwie izometrie spełniają jakąś nietrywialną zależność (są ze sobą przemienne, jedna jest potęgą drugiej etc.) ?

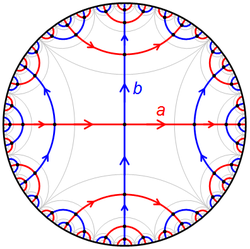
Wariant pierwszego doprowadzi nas do badania tzw. grup Coxetera (tutaj: skończonych grup generowanych przez odbicia) za pomocą grafów. Odpowiedź na drugie pytanie dla przestrzeni trójwymiarowej pozwala uzyskać paradoks Banacha-Steinhausa - kulę trójwymiarową można rozłożyć na skończenie wiele puzzli, z których można złożyć jednocześnie dwie kule rozmiaru wyjściowej. Tej konstrukcji nie da się jednak powtórzyć w dwóch wymiarach. My przyjrzymy się geometrii hiperbolicznej, jej izometriom, kafelkowaniom i zrozumiemy m.in. podział na "kwadraty" (narysowany z lewej strony), który pozwala wnioskować o braku takiej nietrywialnej "relacji" między izometriami \(a\) i \(b\).

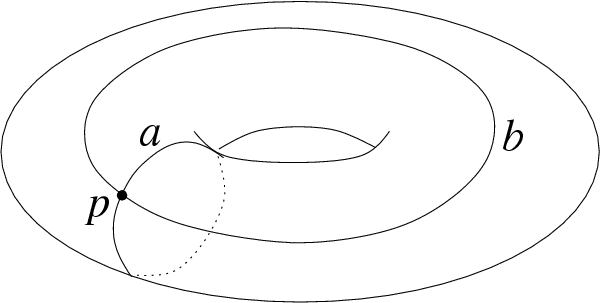Tutaj też na scenę wejdą grupy wolne i, ogólniej, skończenie prezentowalne, które z jednej strony dają się opisać przez kombinatorykę słów, a z drugiej - przez sklejanie ze sobą pętli, którym pozwalamy przechodzić tylko przez pewne ustalone punkty przestrzeni (co może oznaczać, że "pozwalamy" im "korzystać" tylko z pewnych gotowych odcinków, ale może też chodzić o to, że pętla leży np. na butelce Kleina, ew. torusie (powierzchni obwarzanka)), czyli jako tzw. grupa podstawowa. Zobaczymy w ten sposób, jak 2 niezależne od siebie elementy w grupie (np. obroty) prowadzą do nieskończenie wielu niezależnych elementów. Na rysunku po prawej przedstawiono pewne pętle  \(a\) i \(b\) na torusie, wychodzące z punktu \(p\). Zbieżność oznaczeń na obydwu rysunkach nieprzypadkowa ;)

Być może dowiemy się również:

- jak dowodzić własności grupy przez zinterpretowanie jej elementów jako automorfizmów pewnego grafu,

- co to są grupy losowe,

- dlaczego elementarne pytania o grupy mogą być za trudne dla komputerów,

- gdzie tu się chowa teoria liczb.

Wymagania

Potrzebną wiedzę sprawdzają zadania kwalifikacyjne: należy (spróbować) rozwiązać (przynajmniej) część z nich. Próg kwalifikacji nie przekroczy 7 punktów, ale warto spróbować rozwiązać wszystkie zadania.

W rozwiązaniu zadań pomoże skrypt, który potencjalnie zawiera więcej, niż potrzeba do samych zadań, ale przeczytanie go całego może być przydatne do lepszego skorzystania z zajęć.

Rozwiązania polecam przesyłać na adres mailowy orlef.damian [na] gmail.com, najlepiej z tytułem wiadomości zaczynającym się od [WWW11]. Proszę nie używać formatu .docx, najprzyjemniej jest dostawać .pdfy (mogą być skany odręcznych rozwiązań). Można je przesyłać do 5 lipca (do 23:59:59).

Kontakt

Zachęcam do zadawania pytań o zadania/skrypt/zajęcia/cokolwiek na orlef.damian [na] gmail.com.

Zobacz też

Warsztaty Krystalografia dostarczą z pewnością niezapomnianych wrażeń wszystkim zainteresowanym skończonymi podgrupami grupy izometrii przestrzeni trójwymiarowej.