dx, ale czym właściwie jest d?

Opis

Spotkałeś się na pewno z tajemniczym symbolem `dx` przy całkach. Może nawet umiesz sprawnie całkować i różniczkować funkcje. Ale czy zastanawiałeś się kiedyś, co tak naprawdę oznacza `dx`? Czy to tylko kawałek notacji, czy może coś więcej? A co jeśli powiem Ci, że istnieje cała fascynująca teoria, w której `d` jest potężnym operatorem, a `dx` to dopiero początek?

Na tych warsztatach zanurzymy się w świat form różniczkowych – obiektów, które uogólniają funkcje i pozwalają mierzyć rzeczy w zupełnie nowy sposób. Zobaczymy, jak operator `d` (zwany różniczką zewnętrzną) działa na te formy, odkrywając przy tym zadziwiającą własność: `d` zastosowane dwa razy zawsze daje zero (`d² = 0`)! To nie tylko matematyczna ciekawostka, ale klucz do zrozumienia głębokich związków między analizą, geometrią i topologią. **Aby lepiej zrozumieć te abstrakcyjne koncepcje, będziemy wspólnie rozwiązywać zadania ilustrujące własności form i operatora `d`.

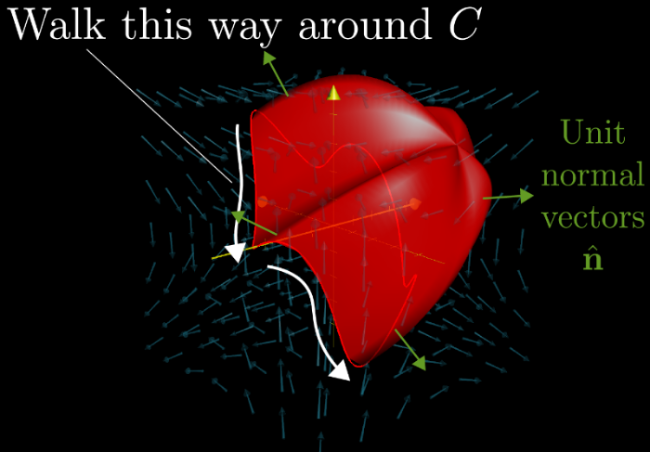
Pokażemy, jak za pomocą form różniczkowych i operatora `d` można badać "dziury" w przestrzeniach (czyli ich topologię), wprowadzając podstawowe idee kohomologii de Rhama. Zobaczysz, jak narzędzia te pozwalają odpowiedzieć na pytania, które wydają się poza zasięgiem standardowego rachunku różniczkowego i całkowego. Co więcej, odkryjemy, że formy różniczkowe i operator `d` pozwalają spojrzeć w nowy, zunifikowany sposób na znane twierdzenia z analizy wektorowej. Poznamy uogólnione twierdzenie Stokesa, które zawiera w sobie jako szczególne przypadki twierdzenie Greena, twierdzenie Gaussa-Ostrogradskiego (o dywergencji) czy podstawowe twierdzenie rachunku całkowego dla całek krzywoliniowych. Zrozumiemy, jak `d` łączy operacje gradientu, rotacji i dywergencji w jedną spójną strukturę.

Jeśli chcesz zobaczyć, jak matematyka łączy różne dziedziny w elegancką całość, odkryć, co kryje się za tajemniczym `dx`, i przećwiczyć nowe idee w praktyce, te warsztaty są dla Ciebie!

Wymagania

Wymagane cechy i umiejętności:

1.    Ciekawość i otwartość na nowe, abstrakcyjne idee matematyczne.
2.   Chęć zrozumienia, co znajduje się "pod maską" znanych narzędzi matematycznych i przećwiczenia tego na zadaniach.
3.   Znajomość pojęcia pochodnej i całki.
4.    Podstawowa intuicja dotycząca wektorów w R² i R³.

Dodatkowe materiały dla zainteresowanych

•   Analiza wektorowa: Dla głębszego zrozumienia gradientu, rotacji, dywergencji oraz twierdzeń Greena, Gaussa i Stokesa (w klasycznej formie) można zajrzeć do książki **Jerrold E. Marsden, Anthony Tromba, "Analiza wektorowa" ("Vector Calculus").Zawiera ona wiele przykładów i dobrze buduje intuicję.
• Analiza na rozmaitościach:Michael Spivak, "Analiza na rozmaitościach" ("Calculus on Manifolds") - klasyczne wprowadzenie do tematyki form różniczkowych.

Uwaga: Wymienione książki prezentują materiał na poziomie akademickim i są pozycjami wymagającymi. Ich lektura jest całkowicie dobrowolna – ani rozwiązanie zadań kwalifikacyjnych, ani pełne uczestnictwo w warsztatach nie wymagają zapoznania się z nimi. Stanowią one jednak doskonałe źródło wiedzy dla osób szczególnie zainteresowanych: mogą posłużyć jako ambitne wprowadzenie przed warsztatami lub jako materiał do pogłębienia zrozumienia tematu już po ich zakończeniu.

Kontakt

W razie jakichkolwiek wątpliwości, uwag, pytań pisz na adres: pm.dudziak@student.uw.edu.pl.